Coding Patterns: Merge Intervals
In Coding Patterns series, we will try to recognize common patterns underlying behind each algorithm question, using real examples from Leetcode.
Previous posts were about Sliding Window, Two Pointers and Fast & Slow Pointers patterns and today, we will introduce Merge Intervals pattern which is very useful to solve the problems involve intervals, overlapping items that need to be merged etc.
Problem: Merge Intervals
LeetCode 56 - Merge Intervals [medium]
Given a collection of intervals, merge all overlapping intervals.
Example 1:
Input: [[1, 3], [2, 6], [8, 10], [15, 18]]
Output: [[1, 6], [8, 10], [15, 18]]
Explanation: Since intervals [1, 3] and [2, 6] overlaps, merge them into [1, 6].
Example 2:
Input: [[1, 4], [4, 5]]
Output: [[1, 5]]
Explanation: Intervals [1, 4] and [4, 5] are considered overlapping.
Merge Intervals Solution
Given two intervals A and B, there will be six different ways the two intervals can relate to each other:

If a.start <= b.start, only 1, 2 and 3 are possible from the above scenarios.
Our goal is to merge the intervals whenever they overlap. For the two overlapping scenarios 2 and 3, this is how we will merge them:
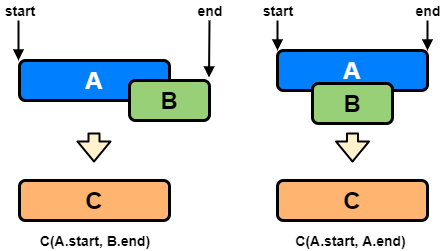
We are going to merge them into a new interval c such that;
c.start = a.start
c.end = max(a.end, b.end)
Here is what our code will look like:
class Solution:
def merge(self, intervals):
if len(intervals) < 2:
return intervals
intervals.sort(key=lambda x: x[0])
merged = []
start = intervals[0][0]
end = intervals[0][1]
for i in range(1, len(intervals)):
interval = intervals[i]
if interval[0] <= end: # overlapping intervals
end = max(interval[1], end)
else: # non-overlapping interval, add the previous interval and reset
merged.append([start, end])
start = interval[0]
end = interval[1]
merged.append([start, end]) # add the last interval
return merged
Time Complexity: O(N * log N) where N is the total number of intervals. In the beginning, since we sort the intervals, our algorithm will take O(N * log N) to run.
Space Complexity: O(N), as we need to return a list containing all the merged intervals.
How to identify?
This approach is quite useful when dealing with intervals, overlapping items or merging intervals.
When the problem involves these clue words, you should think about Merge Intervals pattern.
